|
|
|
|
|
|
|
|
|
|
|
|
Is the frequency of the
digits found in π truly random?
First, I must explain that many would consider π a "pseudo-random"
number, since the number is, after all, always the same. The same pattern of
digits is arrived at each time we calculate π to a set number of decimal
places; otherwise it would be useless as a means of checking the accuracy of
our computers and the programs we run on them. What we are actually examining
then is the appearance of "randomness"
within a fixed number.
So I'll ask instead, "Does π's fixed pattern of digits appear as a random
stream?" Generally speaking, I would have to say, "Yes." However,
depending upon which particular decimal place of π that we stop to add up
each of its ten digits1, we may find some
peculiarities leading the average person to wonder if this is true. Note that
in each of the four bar graphs above, the digits zero and seven
appear to be doing 'rather poorly' at 'breaking even,' and the digits five
and six come up to 'the even mark' only once. The digit three
is characteristic of that which most people would like to see for all of the
digits in a random stream: just a little above or below or 'right
on the money' for each sampling. Whereas the digit one appears as if
its 'racing to be #1' in the frequency count! It increases from
only 1 to 16 counts above the mark, and is never below it. Four and eight
are somewhat similar to three. And the digits two and nine are
always 'over the mark' for these samplings.
|
|
At 10,000
decimal places (see the bar graph above), we find that the digits two
and nine are still 'well over the mark,' and the digits zero and
seven are still 'doing quite poorly' in 'reaching the mark.' But there
are some significant differences as well: Although the digit one is nicely
ahead of almost all the others, the digit five is now far beyond
it and has become the new #1 in this 'race against the odds.'
Also note that the digit eight is now 'far behind' all the others!
The idea of what a truly random number consists of must be examined.
Random does not mean that every time we examine
large numbers of various lengths, each of the digits must have the same frequency!
If this were the case, then many of the patterns we now find in
the digits of π would disappear. Without some differences (including large
differences at times) in digit-frequency between various samplings, it would
be impossible for patterns such as '77777777' to appear. As a matter of fact,
a large number with nearly constant digit-frequencies for each sampling length
might be a very NON-random number, such as, the digits 0-9 simply repeating
over and over again!
What I've tried to show here is that we can use the various
digit-frequency graphs as a guide in helping us to determine the
randomness of π.
I wish that I had the time and talent to develop a computer
program which would be able to take into account all the distribution data for
each and every decimal place of π up to a rather large expansion, say at
least 50 billion digits (the record set in 1999 was already
over 206 billion!2). This might provide us with enough data to arrive at a meaningful conclusion,
at least inductively, about the randomness of π. By having a computer quickly
review the variations in the frequencies at each digit, like watching a movie,
I believe we'd come to the conclusion that π is indeed random. (Since I'm
no "expert" in this field, it may very well be that such data already
exists. For some further musings by a mathematician on questions about the Normality
and Randomness of π see: Is
Pi Normal? by Stan Wagon.)
If you would like to examine some data about π's digit
frequencies, I do have a table here which lists 55 different distribution samples
with all the statistics for each digit; it also includes the CHI-Square
( χ²) for each sampling:
55 Frequency Distributions
for the Digits of π up to
3 billion ( 3,000,000,000 ) Decimal Places.
As is often the case in Mathematics, in order to understand the
randomness π, one must also have a good concept of infinity. Although I believe
that an infinite expansion of π would result in no significant difference
for the variations in the frequency of its digits, proving that this is actually
the case is certainly beyond my abilities. This may help to explain why some
people are still hunting for messages in the latest calculations of π.
One thing I'm sure of: we will always be short of infinity, so it's anyone's
guess as to how far off from an even distribution (or close) that some particular
decimal place of π may become before it swings back in the opposite direction.
Although I'm looking forward to some delightfully interesting patterns yet to
be discovered in π, I doubt you'll ever find any "hidden messages"
in it.
Question: "Are there any known points within π at which all ten of its
digits have exactly the same frequency?" ( I had been thinking about writing
a Perl program to search for this, but now I'm guessing that most likely such
a distribution does not exist. If anyone does find such a decimal place at which
this is true, your name will definitely be honored here.)
"
There's a beauty to Pi that keeps us looking at it...
The digits of Pi are extrememly random. They really have no pattern, and in mathematics
that's really the same as saying they have every pattern."
3
I wonder if anyone has ever developed a fanatical belief in the existence of some
"ultimate" hidden message within the digits of π in the real world.
Since the widespread use of computers, there have also been a number of literary
plots developed around such an idea; a couple have even made it to the
big screen. So, I'm not surprised to find some people who appear
to be overly amazed at the patterns that seem to emerge from this string of numbers.
But there is no special meaning to be found here!
I have always had an interest in the numbers I've come across
in my life, but any possible meaning I might find in them is all coincidence;
something to have fun with, not something I would ever use in making
a decision, or when searching for some spiritual truth! Martin Gardner once
wrote about the similarities that people had found between Abraham
Lincoln and John F. Kennedy after JFK had been assassinated. Then he proceeded to
show that it might be just as easy to find the same number of 'surprising' similarities
for almost any two people if we carefully looked for
them.4
We should enjoy these curious conjunctions for what they are, but
never allow them (or some person proclaiming there's a message in these or any other
numbers, cards, signs in the heavens, etc.) to manipulate us! There are often
some rather amazing coincidences in our lives, but also many magician's tricks which
can be used by con-artists to swindle you.
Since there are only 10 digits in our number system and many different ways in
which we use numbers in our lives (birth, marriage and death dates, ID numbers
like social security or driver's licenses, telephone numbers, credit card numbers,
addresses, etc.) it's actually pretty easy to come across many similarities which
may appear to be significant if you believe that they must be! And
with an infinite stream of random digits to pick and choose from, you should be
able to find ALL of them within the digits of π. For example, it's very easy
to find calendar years and dates of things considered to have great significance.
 |
Keeping all of the above in mind, I'd
like to point out a few digit combinations within the first 1000 decimal places
of π that have caught some people's attention. It's pretty easy to find all
of the binary representations for the decimal numbers 0 through 7; that is 000,
001, 010, 011, 100, 101, 110, and 111. (The sequence 10100 beginning
at the 852nd place giving us three of those.) You'll see many doubled
digits highlighted in yellow and some tripled digits
(including 000 and 111) highlighted in green
[see the illustration above]. If you group the digits into twos or threes, you'll
find a few doublings like 1212 or 9494, and beginning at
the 326th decimal place you'll find 209209.
Someone once asked, "Since π has such a close relationship to a circle
(and using 360 degrees to express its circumference) where do we find the digits
360 in π and is there anything significant about them?" Well
the first 360 begins at the 285th decimal place; nothing interesting
about that. However, the second 360 (you'll find it underlined
with red in the illustration above) begins at the 258th decimal place. This
means the number of degrees in a circle ends up being centered
on the 360th digit of π, so some people think that's significant.
However, this value of 360 in relation to circles is only related to the Babylonian's
sexagesimal (base 60) number system, not an actual relationship
found in nature! So, it's only somewhat interesting because we use degrees more
often than grads or radians or whatever else; it's not truly significant.
(REMEMBER: If it's possible to find some kind of meaning here, people will do
it any way they can! And I'm certain if a '360' had begun
at the 259th decimal place instead, people would simply drop the initial whole
number '3' and talk about how it was centered on 360 decimal places.)
The most interesting pattern here for me is the fact there are six
nines in a row (999999) beginning at the 762nd decimal
place (highlighted with a sky-blue background
in the illustration above). I used to wonder if these digits had been calculated
one by one and if so, what did that person feel like at the time. Imagine their
surprise at finding the digit 9 repeating four, five, and then six times in
a row!
[ I've decided to release the color highlighted table
of Pi's first 1000 decimal places in an HTML version... 1000 Decimal Places of Pi with Color Highlighting.
]
D. F. Ferguson started his calculations of π in 1944 with the aid of a mechanical
"desktop" calculator. At some time in 1945 he arrived at these repeating
nines. Even though he used a machine to do the number crunching, it still took
quite a while for him to arrive at an answer for each of these digits. I don't
have any idea what he was thinking at the time, but since π had already been
proven to be both irrational and transcendental, I'm sure he knew these nines
couldn't continue forever. I do, however, wonder if he ever thought he may have
made a mistake somewhere when he got to the fifth or sixth nine! Pressing on,
he finally ceased his calculations at the 808th digit ( because "e"
-- another very special number in Mathematics -- had previously been
calculated to that length) and awaited verification of his results. By
1948, J. W. Wrench and Levi B. Smith were able to verify all 808 digits. Imagine
having to wait more than two full years for someone to verify your
work!5
π can always provide
us with a necessary diversion, but Life is far too short to spend all your time
searching through these digits!
If you've got the time, here's a site where you can search for patterns of digits
in π ... (Site 1 used the first 10,000,000 digits...)
but Site 2 has recently (since Pi-Day,
March 14th, 2005) been updated to: 200,000,000 decimal places!
Site 1: http://gryphon.ccs.brandeis.edu/~grath/attractions/gpi/
(opens in a new window). Note: The function to use the letter 'd' as a wild
card does NOT appear to be working!
Here's an example of the output you'd get if you searched for the digits 314159
(this site includes the whole number 3 as its first digit ) : SORRY
this site appears to no longer exist!
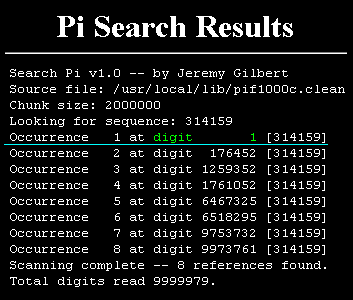
 ResultsThe string 99999999 was found at position 36356642 counting from the first digit after the decimal point. The 3. is not counted.Find Next The string and surrounding digits: 41514034212784215746 99999999 54228236003568972187 This page was brought to you by David G. Andersen [WWW] [Email] Return to the Pi-Search Page. this query took 1.173826 seconds to process |
Footnotes
__________________
1 My observations here have
been limited to the Decimal number system, but one could always expand the research
to include other bases such as Octal or Hexadecimal.
2
In 1997, the record was already over 50 billion.
And in September, 1999, the declared and verified record exceeded 200 billion! This was accomplished using an Hitachi SR8000 with
128 CPUs for a total theoretical peak processing speed of 1 Trillion floating
point operations per second!
3
Statement by Peter Borwein, 1996.
4
Martin Gardner, _ (we're unsure now of the exact reference, it's
probably from the chapter on "Coincidence" in, On Knotted Doughnuts
and Other Mathematical Entertainments, though it could be from any number
of other books which might include the comments of Gardner's Dr. Matrix
character, on this subject; possibly within the book itself entitled: The
Magic Numbers of Dr. Matrix. NOTE: We did finally discover some
specific references to Lincoln and Kennedy on pages 41-45 of this book;
using amazon.com's search program).
5
Some of these facts were found in a paper placed into public domain by Carey
Bloodworth on August 11, 1996.
E-mail
address. (Opens a new window.)
Helping out “thinking people ” since November 8, 1998.
Last Update: 22 May 2007.